今回は前回に引き続き「臨床研究の道標」を読んだ感想を書いていきます。
下巻は研究デザインの型、比較に質などについての実践的な内容が中心となっています。
臨床研究する上では必読の一冊と言えるでしょう。
デザインの種類
ここだけで一冊になりそうな重厚な内容をシンプルにまとめています。
今回取り扱っているデザインとしては「記述研究」「横断研究」「コホート研究」「ケースコントロール研究」「介入研究」という区分にしていました。
まずは今回扱った研究についての分類を見やすい図にしてみます。
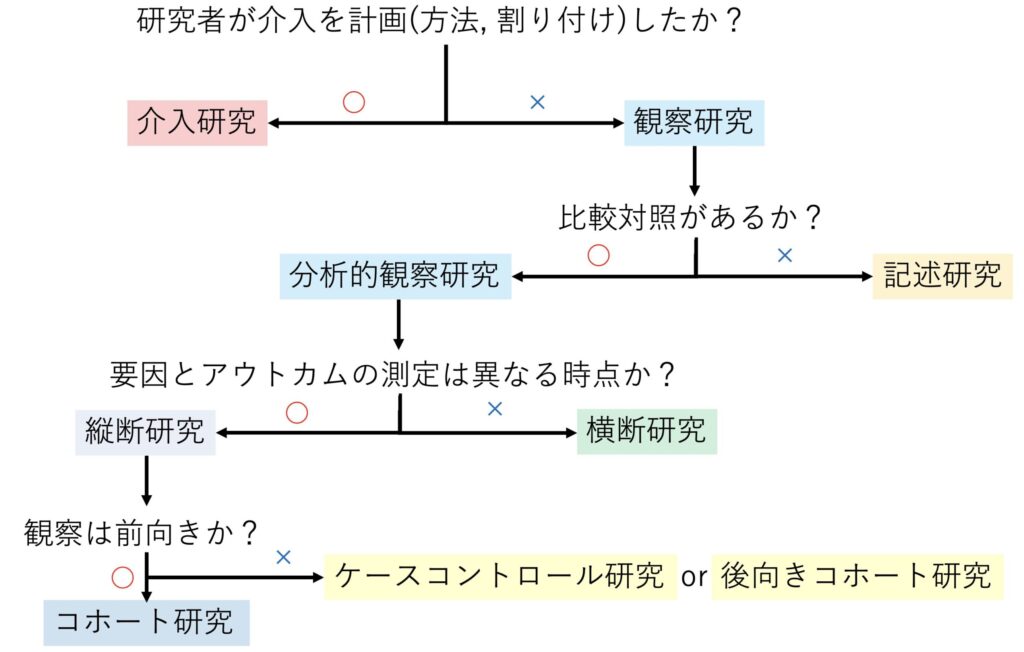
もちろんこれだけではありませんが、だいぶ見やすくなりますね。
デザインで初学者が躓く理由は、この名前の分かりにくさだと思います。
「縦断研究」や「分析的観察研究」といった総称の呼び名があるのが、余計にややこしいですね。
次にこれらの特徴をまとめます。
コホート研究
筆者は特にコホート研究(その中でも筆者が「過去起点コホート」とも呼ぶ「後向きコホート」)を臨床研究では勧めています。
コホート研究が優れている点として以下の4つを挙げています。
- 要因を先に、アウトカムをその後に測定するため時間的関係が明らかである。
- 前向きコホートの場合は結論を歪める交絡因子を事前に検討し、測定しておくことができる。
- 発生の指標であるリスクや発生率を直接計算できる。
- 効果や害を示す指標として、リスク比や発生率比だけでなくリスク差や発生率差も計算することができる。
何よりもリスク差や発生率差という臨床的により役にたつ指標も計算できる点が素晴らしいです。
研究のための研究ではなく、臨床現場に役立てることが本来の目的のはずですからね。
既存のデータを利用するため実現可能性も極めて高い一方、測定していない要因や第3の因子については解析できないことは欠点になります。
ケースコントロール研究
古典的なケースコントロール研究は最初にケースとコントロールを決め、過去の情報から要因を比較するデザインです。
コホートと比べても非常に効率が良いデザインですが、1番の問題点は「コントロール群の設定」です。
同じ病院に通う発症していない人が良いのか、地域全体が良いのか、そしてそうであれば実現可能性はどうなのか。。。
理想とするコントロールを作ることは非常に難しいと知られています。
またケース群では過去のことを思い出しやすいため、「思い出しバイアス」が問題になります。
あとは指標としてもリスクを求めることはできません。
なぜなら前述の通りコントロール群を自分で好きに選んでいるからです。
これでは恣意的な数字になるので、リスクとは出来ないですね。
計算する意義もありません。
ただオッズ比についてはアウトカムの発生が稀であれば、リスク比に近似することが知られています。
コホートとケースのハイブリッド?!
コホート研究は素晴らしいデザインなのですが、反面アウトカムの発生が少ない場合に困ってしまったりアウトカムを起こさない人たちの追跡に多くの労力が必要になる点もデメリットです。
そこで効率化のために考えられたのが、コホートの一部のみをコントロールとして活用する「コホート内ケースコントロール研究」です。
これがさらにネスティッドケースコントロール研究やケースコホート研究というデザインにも分類されます。
偶然誤差と系統誤差
研究する上で大敵になるのは「誤差」です。
ではこれをどのように調整すれば良いでしょうか。
まずは正しく分類するところからですね。
筆者も触れていますが、かなり誤用が多いです。
「誤差」は「系統誤差(広義のバイアス)」と「偶然誤差」に分けられます。
偶然誤差は、上にも下にもずれることのあるエラーです。
本文では繰り返し測定した時の身長で例えています。
一方で系統誤差は、一貫してずれるエラーです。
本文では靴を履いたままの身長測定を持ち出しています。
・・・当然、背は高く計測されますね。
また系統誤差(広義のバイアス)は狭義のバイアスと交絡に分けて考えることもできます。
ここで注意なのは、バイアスは後から調整できないことです。
デザインの時点で考えておかないと、解析などではどうにもなりません。
最強と言われるRCTでも交絡なら未測定のものまで調整できますが、バイアスには対応できません。
この違いも非常に重要ですね。
p値や95%区間の誤解
p値は非常に勘違いされがちな指標です。
なぜ混乱を生むかというと、「効果の大きさ」と「効果の大きさの推定の精度」という2つの情報を1つの指標で表そうとしているからです。
これには無理がありますよね。
つまりどんなに大したことのない差であったとしても(血圧が0.1mmHg下がるとか)サンプルサイズが大きければ偶然誤差は無くなり、p値が小さくなるのです。
逆にいうと効果量が大きくてもサンプルが極端に小さければ、有意差はなかなか付きません。
これらの判断には「効果の大きさ=点推定」、「推定精度=区間推定」という2つの情報が追加されると、より解釈しやすくなります。
ですので本来p値なんてオマケみたいなもので、点推定値と信頼区間が大事になりますね。
この辺りの理解がされないことを「有意差病」と呼んでいるのは非常に言い得て妙な表現でした。
さて、いかがでしたでしょうか。
今回は臨床研究を始めるにあたっての注意点や結果の見せ方について部分的に解説しました。
特に後半は統計解析の根幹に関わる概念になりますので、是非直接お手にとって読んで頂ければと思います。
研究って歪めようと思えばいくらでもねじ曲げられます。
他にも色々な例が書かれていたので、ぜひご覧になってみてください。
そして騙す側でも騙される側でもなく、正しく発信する側になれるように努力していきたいですね。
本日はこの辺で、ではでは。


コメント